Pascal's Triangle

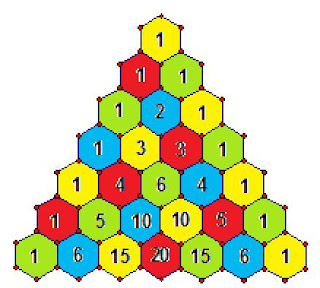
Discovered by a Chinese man in the mid 1200's, the triangle most popularly known as Pascal's Triangle has been the source of answers to many mathematical questions. It is a simple triangle to create, made up of numbers rather than line segments. Here, the "cells" of the triangle are depicted as hexagons, as they make the most pleasing geometric representation of the triangle possible. However, the triangle can be drawn without the hexagons, using numbers only.

Can you see how to create the next few lines? Take a moment to figure it out before reading on.

---

Now that you've studied the triangle, you might have discovered that any cell can be created by adding together the two cells immediately above it. For example, to form the 10 (circled in red) you simply add the values of the cells above and adjacent to it, the 4 and the 6 (circled in blue). The only exception to this rule is the cells that line the two edges of the triangle -- these all contain 1's. So the next row in the triangle would be...1, 7, 21, 35, 35, 21, 7, 1.

Here's an image with extra rows in it that you can continue filling in. Print it as big as possible, because the numbers in those inner cells are going to get pretty darn big, pretty fast! You should also print out a few that you don't fill in for the activities below.

Suggested Activities:

1. Write down as many observations about the triangle as you can.


2. Add up the numbers in each row of the triangle. What pattern do you see in the sums? Make a prediction about the sum of the elements in the 50th row.


3. Add up the numbers in each of the colored diagonals, beginning with the first yellow diagonal, then the red diagonal following it, then the green diagonal following that, then the blue diagonal following that, and so on. Do you see a pattern in the numbers you get? Do you know the name of this number pattern? (You may have to continue the triangle for several more rows, shading in the rest of the diagonals, to find the pattern.)


4. Continue the triangle for several more rows, maybe up to row 20 or so and make some copies of it. Shade all of the cells which contain odd numbers. What do you notice? Do you know the name for this image?


5. On a fresh copy of your large triangle, shade in the cells that are multiples of 5. What do you notice?


6. Try other multiples on other copies and see what you notice.


7. If you remember some algebra, or if you have algebra students in your household, try figuring out the following binomial expansions: (x + y)⁰; (x + y)¹; (x + y)²; (x + y)³; (x + y)⁴; What do you notice about the coefficients of the terms?


8. If you remember how to calculate combinations, calculate C(0,0), C(1,0), C(1, 1), C(2, 0), C(2, 1) and C(2, 2). What do you notice about these numbers and how they relate to Pascal's Triangle? Can you predict the value of C(4, 2) or C(10, 7)?