Every number can be written as the product of prime numbers. A prime number is simply any number with exactly two factors, 1 and itself. Thus, prime numbers include 2, 3, 5, 7, 11, 13 and so on. Notice, though, that 1 is not a prime number because it has only one factor -- itself. A factor tree is a method for finding ALL of the prime factors of a given number. It gets its name from the branching pattern used to find the prime factors.
General Method:
To create a factor tree for the number n, we begin by finding any two numbers whose product is n. For each number, we determine whether it is prime or not. If it is prime, we circle it and move on, because it cannot be factored further. If it is not prime, we follow the same process, by finding two numbers whose product is the number. The process repeats until all of the numbers left are prime.
EXAMPLE 1: Find the prime factorization of 12.
SOLUTION 1:
Find two numbers whose product is 12. I'll choose 4 and 3.
Since 3 is prime, circle it. It is a dead end.
Now, find two numbers whose product is 4. I'll choose 2 and 2. 
Since both of the 2s are prime, we circle them.
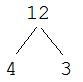
Now that all of the "ends" of the branches are circled, we've found the prime factorization: 2 x 2 x 3 = 12.
Notice that it wouldn't matter if we began with 2 and 6 as our numbers. We would have circled 2 and factored 6 to get 2 and 3, both of which are prime. Again, our prime factorization would be 2 x 2 x 3 = 12.
This leads to an important point: there is exactly one prime factorization of any number. Normally, we write the prime factorization in order from smallest factor to largest. We also use exponents to indicate repeated factors. For instance, the above factorization would actually be written as 22 x 3 = 12.
This leads to an important point: there is exactly one prime factorization of any number. Normally, we write the prime factorization in order from smallest factor to largest. We also use exponents to indicate repeated factors. For instance, the above factorization would actually be written as 22 x 3 = 12.
EXAMPLE 2: Find the prime factorization of 24.
SOLUTION 2:
The two factors I'll choose whose product is 24 are 4 and 6. (But remember, any pair that you start with will lead to the same prime factorization, though not the same factor tree!)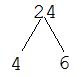
Since niether of these two numbers is prime, I have to factor them both. First, the 4. My two factors are 2 and 2.
Since these are both prime, I'll circle them.
Now, I'll factor the 6, using 2 and 3. 
Since both 2 and 3 are prime, I'll circle them.
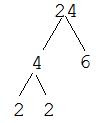
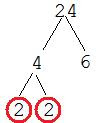
All of the "ends" of the branches are circled, so we have our prime factorization: 2 x 2 x 2 x 3 = 24 or 23 x 3 = 24.
Try your own factor trees. You can verify that you've succeeded simply by multiplying your prime factors. You should get the number you started with.
No comments:
Post a Comment