7.23.2009
Thinking Numerically
As an aside, I was unable to verify this statistic online. Also, I don't know (but suspect) that some of the viruses are constrained by geography, much like other diseases are. So, you may experience a decrease in the number of viruses you contract per year because only a fraction of them exist in your locale, and therefore, you may contract many of them before the end of your life.
7.17.2009
Evens and Odds
Even or Odd?
If I asked you to list some even numbers, you'd probably say, "2, 4, 6, 8, ... do you want me to keep going?"
"No, no, " I'd say. "That's fine."
But what do all of those numbers have in common? Yes, I know. They're even. But what makes them even?
Of course! When you divide them by 2, there's no remainder. In other words, 2 goes "evenly" into each number. Another way to say this is that each number is equal to 2 times some other number. For instance, 8 is even because it is 2 x 4. 12 is even because it is 2 x 6. 2 is even because it is 2 x 1. And even zero is even because it is 2 x 0.
In Algebra, we often represent an unknown even number as 2n. That's because no matter what we choose for n, multiplying it by 2 makes the result even.
So if an even number is "evenly" divided by 2, what's an odd number? It's a number that is NOT "evenly" divided by 2, of course. In other words, there is a remainder when we divide an odd number by 2. But one of the other things that we notice about odd numbers is that they come immediately after the even numbers. In other words, if we just add 1 to an even number, we get an odd number. 9, for instance, comes right after the even number 8. So if 8 is 2 x 4, then 9 must be 2 x 4 +1. We can write all of our odd numbers this way.
In Algebra, we often represent an unknown odd number as 2n + 1. That's because an odd number is always one more than an even number.
Addition Properties:
If you take any two even numbers, say 24 and 8, and add them together, you get another even number, in this case, 32. Try it. Find a bunch of different pairs of even numbers and have at it. Satisified? Ok.
Now how about trying to add any two odd numbers together. Let's take 9 and 17 as an example. We get 26 when we add them, an even number. Does this always happen? Try a bunch of odd number pairs. Go ahead. I'll wait.
Ok, now try adding one even and one odd number together. Yup. Say 8 and 17. That's right, we get 25, an odd number. Once again, test this out with several even/odd pairs to see if it ALWAYS works.
Algebraic Proofs:
Now, you might have convinced yourself that you've discovered some properties of addition:
even + even = even
odd + odd = even
even + odd = odd
But could there possibly be a case for which one of these properties doesn't work? In other words, is there a pair of even numbers that doesn't give you back an even result? In order to know for sure, mathematicians like to prove things, in this case using Algebra.
Let's use our Algebraic representations of even and odd numbers to help us out. We said before that an even number can be represented as 2n and an odd number can be represented as 2n + 1. So, let's uses these two facts to try out our addition facts. Let's start with adding two even numbers.
Conjecture: The sum of two even numbers is even.
Proof:
Let's represent each even number Algebraically. One of them will be 2n and the other will be 2m. (We don't want to make them both be 2n, because that would mean that we are adding an even number to itself. We want to be sure that we can pick two unique even numbers if we want to.)
2n + 2m
We can simplify this a bit by factoring out (or un-distributing, if you remember your distributive property) a 2.
2n + 2m = 2 ( n + m )
Now, we need to ask ourselves if 2 ( n + m ) is even. If we look back at how we described our even numbers, we said that an even number is a number that we can form by multiplying some other number by 2. Well, regardless of what n and m are, if we add them, we definitely get "some other number". And that "some other number" is definitely being multiplied by 2. So, 2 (n + m ) is definitely even.
So, we've just proved, Algebraically, that the sum of two even numbers is ALWAYS another even number.
Conjecture: An odd plus and even is an odd.
Proof:
We need to add an odd and an even. The algebraic representation of an odd number is 2n + 1, and the even number is 2m. Let's add them.
2n + 1 + 2m
A bit of rearranging gives us:
2n + 2m + 1
Now, we just saw, in the previous proof, that 2n + 2m can be turned into 2(n + m), which is even.
2 ( n + m ) + 1
So this little expression is an even number plus 1. Well, that's the description of an odd number, for sure. So by adding an even and an odd, we've managed to get another odd.
Because we don't ever care what someone decides to pick for n and m, this is a proof that ALWAYS works.
Suggested Activities:
- Prove, using Algebra, that the sum of two odd numbers is even.
- Prove, using Algebra, that the sum of an odd number and an even number is odd.
- Develop some rules for multiplying even and odd numbers.
- Prove, using Algebra, your multiplication rules.
7.16.2009
Four Thousand Years Ago in Egypt...
- Write the following in Egyptian numbers: your age; your weight; the year of your birth; the cost of a new Jaguar car (any model); the current population of the state in which you live; the current population of the world.
- See if you can find a way to add two Egyptian numbers together, such as 839 and 427. Don't convert them into our numbers first and then switch back to Egyptian. Think like an Egyptian and use only their symbols. You might discover why we "carry" when we're adding numbers together.
- See if you can find a way to subtract two Egyptian numbers, such as 5493 and 3586. Again, only use Egyptian symbols and don't convert into our number system. You just might discover what "borrowing" really means.
- Write a short essay explaining what happens when you try to write numbers such as 200 or 40,008.
- Find a foolproof method for determining the total number of symbols required to write any number in Egyptian. For example, how many symbols do you need to write the number 2004? 24,489? 9,999,999? Is there a general method you can use that works ALL the time?
- Take a look at this image of the Moscow Papyrus, one of the few Ancient Egyptian mathematical texts in existence. Can you see any numbers?

I'll post an article on addition and subtraction next so that you can check your method against the Egyptian way.
7.08.2009
Pascal's Triangle
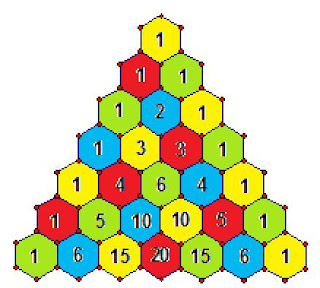
Discovered by a Chinese man in the mid 1200's, the triangle most popularly known as Pascal's Triangle has been the source of answers to many mathematical questions. It is a simple triangle to create, made up of numbers rather than line segments. Here, the "cells" of the triangle are depicted as hexagons, as they make the most pleasing geometric representation of the triangle possible. However, the triangle can be drawn without the hexagons, using numbers only.
Can you see how to create the next few lines? Take a moment to figure it out before reading on.
Now that you've studied the triangle, you might have discovered that any cell can be created by adding together the two cells immediately above it. For example, to form the 10 (circled in red) you simply add the values of the cells above and adjacent to it, the 4 and the 6 (circled in blue). The only exception to this rule is the cells that line the two edges of the triangle -- these all contain 1's. So the next row in the triangle would be...1, 7, 21, 35, 35, 21, 7, 1.
Here's an image with extra rows in it that you can continue filling in. Print it as big as possible, because the numbers in those inner cells are going to get pretty darn big, pretty fast! You should also print out a few that you don't fill in for the activities below.
Suggested Activities:
- Write down as many observations about the triangle as you can.
- Add up the numbers in each row of the triangle. What pattern do you see in the sums? Make a prediction about the sum of the elements in the 50th row.
- Add up the numbers in each of the colored diagonals, beginning with the first yellow diagonal, then the red diagonal following it, then the green diagonal following that, then the blue diagonal following that, and so on. Do you see a pattern in the numbers you get? Do you know the name of this number pattern? (You may have to continue the triangle for several more rows, shading in the rest of the diagonals, to find the pattern.)
- Continue the triangle for several more rows, maybe up to row 20 or so and make some copies of it. Shade all of the cells which contain odd numbers. What do you notice? Do you know the name for this image?
- On a fresh copy of your large triangle, shade in the cells that are multiples of 5. What do you notice?
- Try other multiples on other copies and see what you notice.
- If you remember some algebra, or if you have algebra students in your household, try figuring out the following binomial expansions: (x + y)0; (x + y)1; (x + y)2; (x + y)3; (x + y)4; What do you notice about the coefficients of the terms?
- If you remember how to calculate combinations, calculate C(0,0), C(1,0), C(1, 1), C(2, 0), C(2, 1) and C(2, 2). What do you notice about these numbers and how they relate to Pascal's Triangle? Can you predict the value of C(4, 2) or C(10, 7)?
6.30.2009
On The Importance of Trees
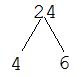
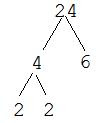
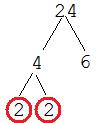
Every number can be written as the product of prime numbers. A prime number is simply any number with exactly two factors, 1 and itself. Thus, prime numbers include 2, 3, 5, 7, 11, 13 and so on. Notice, though, that 1 is not a prime number because it has only one factor -- itself. A factor tree is a method for finding ALL of the prime factors of a given number. It gets its name from the branching pattern used to find the prime factors.
General Method:
To create a factor tree for the number n, we begin by finding any two numbers whose product is n. For each number, we determine whether it is prime or not. If it is prime, we circle it and move on, because it cannot be factored further. If it is not prime, we follow the same process, by finding two numbers whose product is the number. The process repeats until all of the numbers left are prime.
EXAMPLE 1: Find the prime factorization of 12.
SOLUTION 1:
Find two numbers whose product is 12. I'll choose 4 and 3.
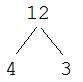
This leads to an important point: there is exactly one prime factorization of any number. Normally, we write the prime factorization in order from smallest factor to largest. We also use exponents to indicate repeated factors. For instance, the above factorization would actually be written as 22 x 3 = 12.