Thinking Numerically

I have heard that there are something like 450 common cold viruses -- those viruses which cause the symptoms of the common cold. This explains why you can keep catching colds even after your body has made antibodies to fight off the infection caused by a previous virus. And, it explains why you keep getting colds, year after year. After all, you'd think that eventually you'd become immune to them. But, think about this. If you live to the average life span of 75, then, in order to contract each cold virus, you'd have to have 450/75 or 6 colds per year, for every year of your life. Since I only get about 2 or 3 a year, now, I'm destined to keep getting colds!

As an aside, I was unable to verify this statistic online. Also, I don't know (but suspect) that some of the viruses are constrained by geography, much like other diseases are. So, you may experience a decrease in the number of viruses you contract per year because only a fraction of them exist in your locale, and therefore, you may contract many of them before the end of your life.

Evens and Odds

Did you know that even numbers are considered female and odd numbers are considered male? The Chinese and the Pythagoreans alike often imbued numbers with personality and human qualities, forming a mystical mathematics alongside the practical and logical mathematics. But there are some interesting properties of odd and even numbers that seldom get discussed. But knowing these properties can help you determine if an answer you arrived at is correct.

Even or Odd?
If I asked you to list some even numbers, you'd probably say, "2, 4, 6, 8, ... do you want me to keep going?"
"No, no, " I'd say. "That's fine."
But what do all of those numbers have in common? Yes, I know. They're even. But what makes them even?

Of course! When you divide them by 2, there's no remainder. In other words, 2 goes "evenly" into each number. Another way to say this is that each number is equal to 2 times some other number. For instance, 8 is even because it is 2 x 4. 12 is even because it is 2 x 6. 2 is even because it is 2 x 1. And even zero is even because it is 2 x 0.

In Algebra, we often represent an unknown even number as 2n. That's because no matter what we choose for n, multiplying it by 2 makes the result even.

So if an even number is "evenly" divided by 2, what's an odd number? It's a number that is NOT "evenly" divided by 2, of course. In other words, there is a remainder when we divide an odd number by 2. But one of the other things that we notice about odd numbers is that they come immediately after the even numbers. In other words, if we just add 1 to an even number, we get an odd number. 9, for instance, comes right after the even number 8. So if 8 is 2 x 4, then 9 must be 2 x 4 +1. We can write all of our odd numbers this way.

In Algebra, we often represent an unknown odd number as 2n + 1. That's because an odd number is always one more than an even number.

Addition Properties:
If you take any two even numbers, say 24 and 8, and add them together, you get another even number, in this case, 32. Try it. Find a bunch of different pairs of even numbers and have at it. Satisified? Ok.

Now how about trying to add any two odd numbers together. Let's take 9 and 17 as an example. We get 26 when we add them, an even number. Does this always happen? Try a bunch of odd number pairs. Go ahead. I'll wait.

Ok, now try adding one even and one odd number together. Yup. Say 8 and 17. That's right, we get 25, an odd number. Once again, test this out with several even/odd pairs to see if it ALWAYS works.


Algebraic Proofs:
Now, you might have convinced yourself that you've discovered some properties of addition:

even + even = even
odd + odd = even
even + odd = odd

But could there possibly be a case for which one of these properties doesn't work? In other words, is there a pair of even numbers that doesn't give you back an even result? In order to know for sure, mathematicians like to prove things, in this case using Algebra.

Let's use our Algebraic representations of even and odd numbers to help us out. We said before that an even number can be represented as 2n and an odd number can be represented as 2n + 1. So, let's uses these two facts to try out our addition facts. Let's start with adding two even numbers.

Conjecture: The sum of two even numbers is even.
Proof:
Let's represent each even number Algebraically. One of them will be 2n and the other will be 2m. (We don't want to make them both be 2n, because that would mean that we are adding an even number to itself. We want to be sure that we can pick two unique even numbers if we want to.)

2n + 2m

We can simplify this a bit by factoring out (or un-distributing, if you remember your distributive property) a 2.

2n + 2m = 2 ( n + m )

Now, we need to ask ourselves if 2 ( n + m ) is even. If we look back at how we described our even numbers, we said that an even number is a number that we can form by multiplying some other number by 2. Well, regardless of what n and m are, if we add them, we definitely get "some other number". And that "some other number" is definitely being multiplied by 2. So, 2 (n + m ) is definitely even.

So, we've just proved, Algebraically, that the sum of two even numbers is ALWAYS another even number.

Conjecture: An odd plus and even is an odd.
Proof:

We need to add an odd and an even. The algebraic representation of an odd number is 2n + 1, and the even number is 2m. Let's add them.

2n + 1 + 2m

A bit of rearranging gives us:

2n + 2m + 1

Now, we just saw, in the previous proof, that 2n + 2m can be turned into 2(n + m), which is even.

2 ( n + m ) + 1

So this little expression is an even number plus 1. Well, that's the description of an odd number, for sure. So by adding an even and an odd, we've managed to get another odd.

Because we don't ever care what someone decides to pick for n and m, this is a proof that ALWAYS works.

---

Suggested Activities:

1. Prove, using Algebra, that the sum of two odd numbers is even.
2. Prove, using Algebra, that the sum of an odd number and an even number is odd.
3. Develop some rules for multiplying even and odd numbers.
4. Prove, using Algebra, your multiplication rules.

Four Thousand Years Ago in Egypt...

If you had been a priest in ancient Egypt, you would have been in the highest class of men. You would have had great power and control over mere mortals and held great sway with the Pharoah. You would have been knowledgeable in many subjects, not the least of which was mathematics. Your ability to reckon and keep records would have made you indispensible. And you would have jealously guarded this secret power, teaching it only to a select few who would work for you and later, perhaps, take your place.

But your ability to reckon would have been nothing like ours. In fact, the numbers you used would have looked completely different. Not only would you have used different symbols, but you would have formed large numbers in a manner much like the Romans would use. You would have used an additive numeration system and thus your techniques for adding and subtracting would have differed vastly from our algorithms.

The Eyptians had only a few symbols with which to create numbers.

The first symbol is called a stroke and is worth just 1, a unit. The second symbol is the heel bone and is worth 10 strokes. The third symbol is the scroll, worth ten heel bones, or 100 strokes. The fourth is a lotus flower and is worth ten scrolls, or 1000 strokes. Fifth is the pointing finger and is worth ten lotus flowers or 10,000 strokes. Sixth is the tadpole, worth ten pointing fingers or 100,000 strokes. And finally is the astonished man, worth ten tadpoles or one million strokes.

To create a number, you add together as many of each symbol as necessary to form the value. For instance, to create the Egyptian number that represents 47, you would need four heel bones and seven strokes. It doesn't really matter which order you put the symbols in, but by convention, the symbols were written in groups ordered from smallest to biggest. So this number would be shown with the seven strokes followed by the four heel bones.

In the same way, you can convert an Egyptian number to our system by adding the values of the symbols together. For example:

Counting the amount of each symbol, we see six strokes, five heel bones, and three scrolls. That makes six 1's, five 10's, and three 100's. In our number system, we'd write that as 356 or three hundred fifty six.

Suggested Activities:

1. Write the following in Egyptian numbers: your age; your weight; the year of your birth; the cost of a new Jaguar car (any model); the current population of the state in which you live; the current population of the world.
2. See if you can find a way to add two Egyptian numbers together, such as 839 and 427. Don't convert them into our numbers first and then switch back to Egyptian. Think like an Egyptian and use only their symbols. You might discover why we "carry" when we're adding numbers together.
3. See if you can find a way to subtract two Egyptian numbers, such as 5493 and 3586. Again, only use Egyptian symbols and don't convert into our number system. You just might discover what "borrowing" really means.
4. Write a short essay explaining what happens when you try to write numbers such as 200 or 40,008.
5. Find a foolproof method for determining the total number of symbols required to write any number in Egyptian. For example, how many symbols do you need to write the number 2004? 24,489? 9,999,999? Is there a general method you can use that works ALL the time?
6. Take a look at this image of the Moscow Papyrus, one of the few Ancient Egyptian mathematical texts in existence. Can you see any numbers?

I'll post an article on addition and subtraction next so that you can check your method against the Egyptian way.

Pascal's Triangle

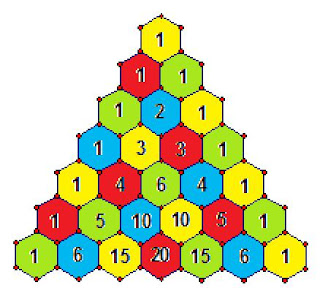
Discovered by a Chinese man in the mid 1200's, the triangle most popularly known as Pascal's Triangle has been the source of answers to many mathematical questions. It is a simple triangle to create, made up of numbers rather than line segments. Here, the "cells" of the triangle are depicted as hexagons, as they make the most pleasing geometric representation of the triangle possible. However, the triangle can be drawn without the hexagons, using numbers only.

Can you see how to create the next few lines? Take a moment to figure it out before reading on.

---

Now that you've studied the triangle, you might have discovered that any cell can be created by adding together the two cells immediately above it. For example, to form the 10 (circled in red) you simply add the values of the cells above and adjacent to it, the 4 and the 6 (circled in blue). The only exception to this rule is the cells that line the two edges of the triangle -- these all contain 1's. So the next row in the triangle would be...1, 7, 21, 35, 35, 21, 7, 1.

Here's an image with extra rows in it that you can continue filling in. Print it as big as possible, because the numbers in those inner cells are going to get pretty darn big, pretty fast! You should also print out a few that you don't fill in for the activities below.

Suggested Activities:

1. Write down as many observations about the triangle as you can.


2. Add up the numbers in each row of the triangle. What pattern do you see in the sums? Make a prediction about the sum of the elements in the 50th row.


3. Add up the numbers in each of the colored diagonals, beginning with the first yellow diagonal, then the red diagonal following it, then the green diagonal following that, then the blue diagonal following that, and so on. Do you see a pattern in the numbers you get? Do you know the name of this number pattern? (You may have to continue the triangle for several more rows, shading in the rest of the diagonals, to find the pattern.)


4. Continue the triangle for several more rows, maybe up to row 20 or so and make some copies of it. Shade all of the cells which contain odd numbers. What do you notice? Do you know the name for this image?


5. On a fresh copy of your large triangle, shade in the cells that are multiples of 5. What do you notice?


6. Try other multiples on other copies and see what you notice.


7. If you remember some algebra, or if you have algebra students in your household, try figuring out the following binomial expansions: (x + y)⁰; (x + y)¹; (x + y)²; (x + y)³; (x + y)⁴; What do you notice about the coefficients of the terms?


8. If you remember how to calculate combinations, calculate C(0,0), C(1,0), C(1, 1), C(2, 0), C(2, 1) and C(2, 2). What do you notice about these numbers and how they relate to Pascal's Triangle? Can you predict the value of C(4, 2) or C(10, 7)?

On The Importance of Trees

Factor trees are possibly the most useful tool for problems involving multiplication and division. From finding least common denominators and greatest common factors to simplifying nth roots and finding proper divisors, this simple tool generates results quickly and accurately every time.

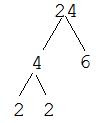
Every number can be written as the product of prime numbers. A prime number is simply any number with exactly two factors, 1 and itself. Thus, prime numbers include 2, 3, 5, 7, 11, 13 and so on. Notice, though, that 1 is not a prime number because it has only one factor -- itself. A factor tree is a method for finding ALL of the prime factors of a given number. It gets its name from the branching pattern used to find the prime factors.

General Method:
To create a factor tree for the number n, we begin by finding any two numbers whose product is n. For each number, we determine whether it is prime or not. If it is prime, we circle it and move on, because it cannot be factored further. If it is not prime, we follow the same process, by finding two numbers whose product is the number. The process repeats until all of the numbers left are prime.

---

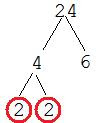
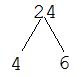
EXAMPLE 1: Find the prime factorization of 12.

SOLUTION 1:
Find two numbers whose product is 12. I'll choose 4 and 3.

Since 3 is prime, circle it. It is a dead end.

Now, find two numbers whose product is 4. I'll choose 2 and 2.

Since both of the 2s are prime, we circle them.

Now that all of the "ends" of the branches are circled, we've found the prime factorization: 2 x 2 x 3 = 12.

Notice that it wouldn't matter if we began with 2 and 6 as our numbers. We would have circled 2 and factored 6 to get 2 and 3, both of which are prime. Again, our prime factorization would be 2 x 2 x 3 = 12.

---

This leads to an important point: there is exactly one prime factorization of any number. Normally, we write the prime factorization in order from smallest factor to largest. We also use exponents to indicate repeated factors. For instance, the above factorization would actually be written as 2² x 3 = 12.

---

EXAMPLE 2: Find the prime factorization of 24.

SOLUTION 2:

The two factors I'll choose whose product is 24 are 4 and 6. (But remember, any pair that you start with will lead to the same prime factorization, though not the same factor tree!)

Since niether of these two numbers is prime, I have to factor them both. First, the 4. My two factors are 2 and 2.

Since these are both prime, I'll circle them.

Now, I'll factor the 6, using 2 and 3.

Since both 2 and 3 are prime, I'll circle them.

All of the "ends" of the branches are circled, so we have our prime factorization: 2 x 2 x 2 x 3 = 24 or 2³ x 3 = 24.

---

Try your own factor trees. You can verify that you've succeeded simply by multiplying your prime factors. You should get the number you started with.

What if Humans Only Had 8 Fingers?

Most cultures developed a base ten counting system because we have, well, ten fingers. Imaging a prehistoric tribe which needs to count its members for the annual census. In order to accomplish the task, each member of the tribe would file past the tribal elders, one by one, while they did the counting. Now, since most prehistoric peoples only had number words for one, two and many, it would be awefully hard to get an accurate count using these few words. So instead, as the first person files past, the Tribal Counter would hold up one finger. As each of the next nine people came by, he would hold up another finger until all 10 of his fingers were raised. At this point, one of two things could happen:

• A second tribal counter could begin holding up each of his fingers for the next ten members, enabling a count up to 20, or
• A second tribal counter could hold up one finger to indicate that the first tribal counter had reached a full count, and then the first tribal counter could lower all of his fingers to prepare to count the next ten members.

If the first method is used, then it would take ten men to count 100 tribe members. If the second method is used, then it would take only two men to count 100 tribe members. The second method is the one that allows us to so neatly express quantities today.

Now, imagine that the tribe has 228 members. After the first tribal counter has run through his fingers ten times, the second tribal counter has all of his fingers raised. If the first tribal counter continues on the the eleventh set of ten, then the second tribal counter will not have enough fingers to keep track of this next group of ten. So, we need a third tribal counter to keep track of how many times the second tribal counter has lifted all of his fingers. When the second tribal counter has reached a full count, the third tribal counter raises one finger, while the second tribal counter returns his fingers to the down position. If you imagine him with closed fists, you can easily see how the number 100 is generated: the first and second counter's have their fists closed while the third has one finger raised. In the end, after all of the members had been counted, the first man would be holding up eight fingers, the second would be holding up two and the third would be holding up two. It would then be easy for us to read and recognize this number as 228.

But what if we only had 8 fingers to count on? What would change about our counting systems? Imagining the same scenarioas above, when the first tribal counter gets to 8, he has run out of fingers and must ask the second tribal counter to hold up one finger, while he returns his to the closed fist position. Now, we would see 10, even though it only represents 8 men. How many times could the first counter raise all of his fingers before using up all of the fingers of the second counter? Eight times, of course. Since each raised finger on the second man represents a group of 8 from the first man, this means that a full count on the second man represents a total of 64 people; when the third man raises his finger and the second man returns his to the closed fist position, we see 100 represented on their hands, but it really only means that 64 people have been counted. Therefore, the first man represents the ones place, the second man represents the eights place and the third man represents the sixty-fours place.

If we think of these numbers using the symbols we currently use to count with, we would see the written numerals as follows:

1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 24, 25, 26, 27, ..., 100, 101, 102, 103, 104, 105, 106, 107, 110, 111, 112...

Now, 10 does not mean ten, but eight.

Of course, it's easy to get confused because we're using the symbols that we use for a base 10 system, so numbers in a base 8 system can't be spoken the same way. A new vocabulary of number words would have to be created to match the meaning of the symbols.

---

Suggested Activities

1. The digits used in a base 10 numbering system are 0 through 9. What are the allowable digits in a base 8 system? How about in a base 3 system?
2. How would you create enough symbols to represent all of the allowable digits in a base 16 numbering system? Remember, a digit can only be a single symbol, not a combination of other symbols.
3. What would the place values of a base 3 system be? What would the place values of a base 16 system be?
4. Try counting in base 3. List the first 20 numbers on a sheet of paper. Now list the first 20 numbers in a base 8 system. And finally, list the first 20 numbers in a base 16 system.

Welcome

After years of studying math and math history, I find myself with a large store of information and a limited audience with which to share it. So, it is with a love of math and teaching that I bring to you Math Stuff -- Things You Never Learned in School.... I hope you'll find it to be enjoyable, useful and intriguing.